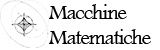“Ruotati il vitreo attorno alla propria base come asse e la linea dell’osservatore attorno al piede in modo che la linea dell’osservatore resti sempre parallela alla retta nel vitreo perpendicolare alla base di questo: l’immagine del punto da disegnare, dato nel pavimento, appare nel vitreo sempre al medesimo posto”. (Così avviene anche, quindi, per l’immagine di una figura da disegnare situata sul pavimento)
Proiezioni e ombra di figure piane

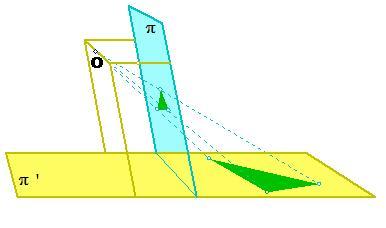
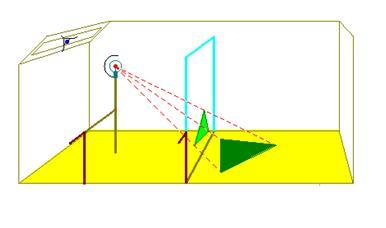
Prima parte ( a destra nella fotografia). Il parallelepipedo articolato permette di muovere contemporaneamente punto di vista e quadro mantenendo invariata l'immagine prospettica della figura giacente sul piano di terra. (Il quadro π ruota attorno alla linea di terra; il punto di vista O descrive una circonferenza avente come centro l’intersezione tra il piano di terra π’ e la retta per O parallela a π.
Seconda parte (a sinistra nella fotografia). Il meccanismo è identico (controllare aprendo lo sportello), ma ora sposta una lampada puntiforme insieme a un quadro in cui sono praticate due aperture: i contorni delle ombre proiettate rimangono immutati . (Teorema di Stevin, 1605).
Proiezione di una circonferenza in ellissi

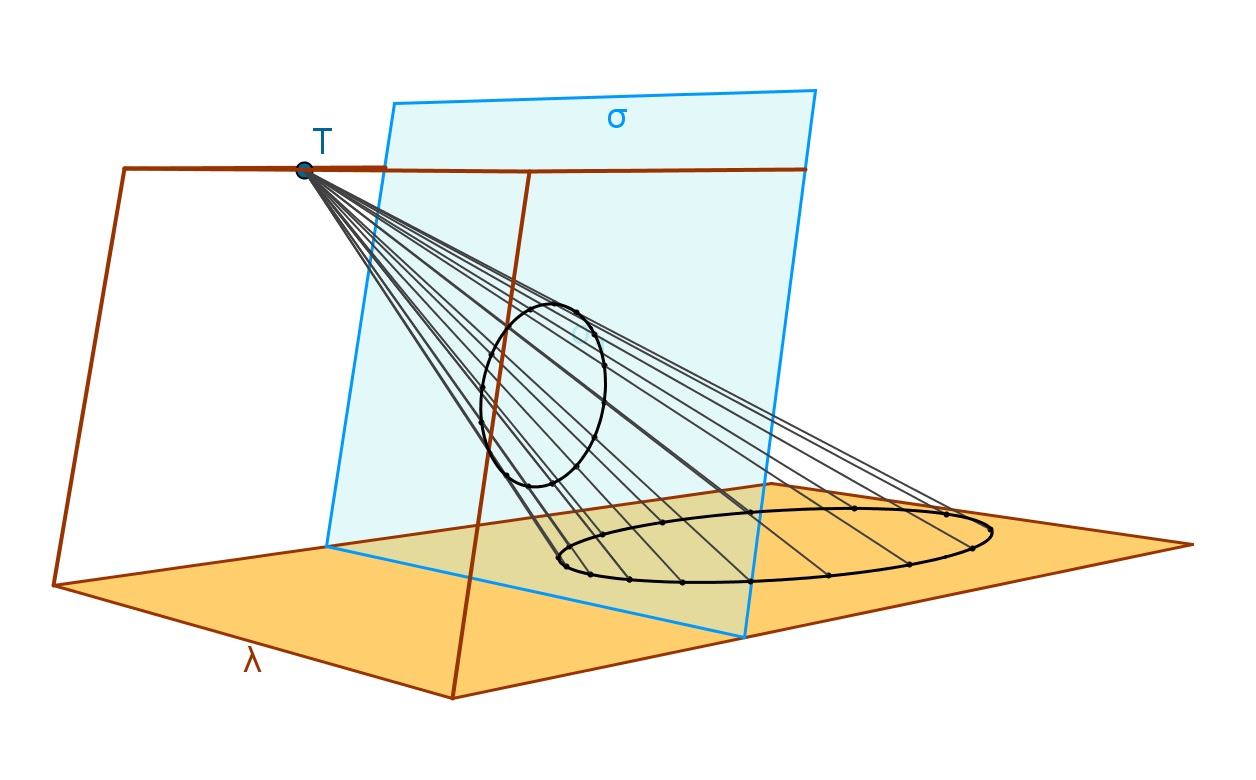
A partire dai primi decenni del Seicento, dopo gli studi fondamentali di G. Del Monte, B. Pascal e G. Desargues, la trattazione delle coniche viene inserita entro la teoria delle proiezioni. Le coniche infatti si possono considerare come ombre (o prospettive, o anamorfosi) delle circonferenze.
In questo modello fisico i fili tesi possono essere interpretati sia come raggi visuali convergenti all’occhio di un osservatore, sia come raggi luminosi uscenti da una sorgente puntiforme. Essi stabiliscono una corrispondenza tra i piani incidenti σ e λ sono corrispondenti i punti collegati dal medesimo filo. Possiamo anche dire: ogni filo proietta un punto di σ in un punto di λ; centro di proiezione è il punto di convergenza dei fili.
Il modello mostra che la circonferenza giacente sul piano σ è proiettata sul piano λ da un centro proprio (non appartenente né a σ né a λ in modo da ottenere una ellisse. Possiamo anche dire: la circonferenza è immagine prospettica dell’ellisse; l’ellisse è ombra della circonferenza.
Il piano della circonferenza e il centro di proiezione possono essere ruotati contemporaneamente per mezzo di un parallelepipedo articolato in modo tale che la corrispondenza tra ellisse e circonferenza rimanga invariata (Teorema di Stevin). Si noti che σ ruota attorno alla propria intersezione con λ(retta luogo di punti uniti).
Proiezione di una circonferenza in parabola

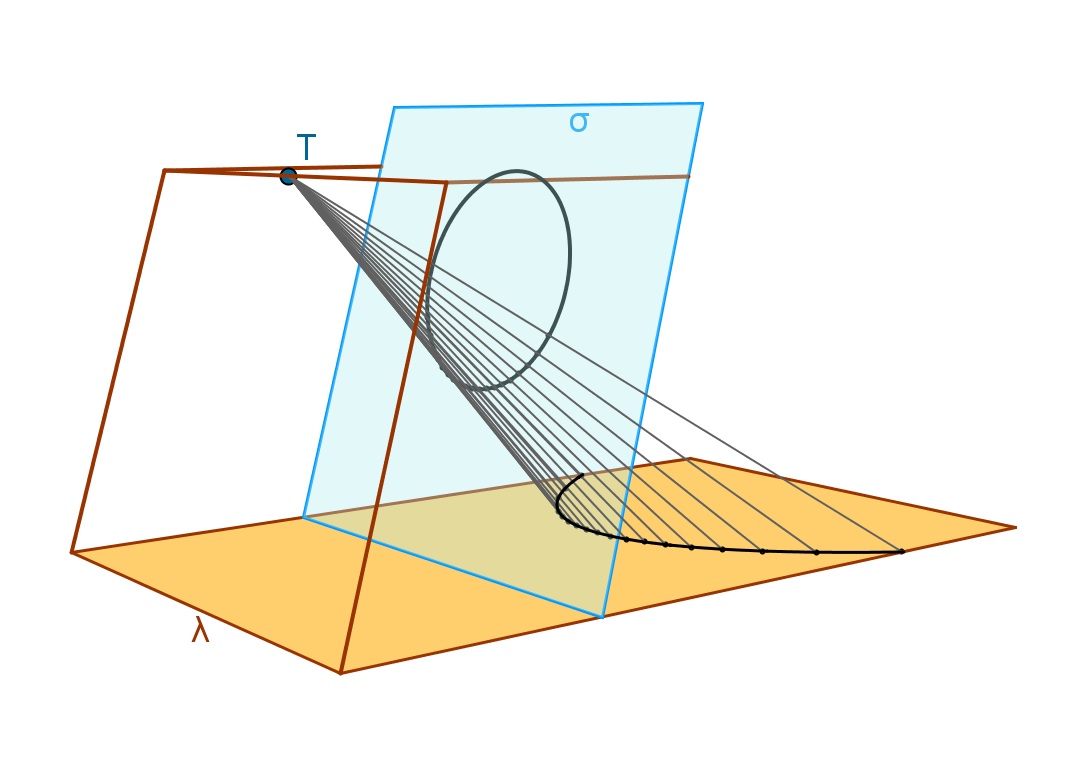
In questo modello fisico (i fili rappresentano raggi visuali o raggi luminosi) una circonferenza viene trasformata in parabola da una prospettività (con centro proprio) tra due piani incidenti σ e λ.
La circonferenza tracciata su σ è tangente alla retta limite di σ (retta intersezione tra σ e il piano parallelo a λ condotto dal centro della prospettività).
Nel modello, il piano della circonferenza e il centro di proiezione possono essere assoggettati ai movimenti previsti dal teorema di Stevin. Completando il ribaltamento di σ su λ, la parabola apparirebbe come trasformata della circonferenza in una omologia.
Proiezione di una circonferenza in iperbole

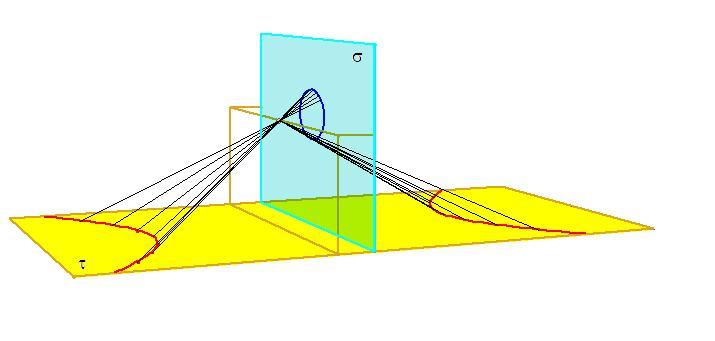
In questo modello fisico (i fili rappresentano raggi visuali o raggi luminosi) una circonferenza viene trasformata in iperbole da una prospettività (con centro proprio) tra due piani incidenti σe τ. La circonferenza tracciata su σ, interseca in due punti la retta limite di σ (retta intersezione tra σ e il piano parallelo a τ condotto dal centro della prospettività).
Nel modello, il piano della circonferenza e il centro di proiezione possono essere assoggettati ai movimenti previsti dal teorema di Stevin. Completando il ribaltamento di σ su τ, l’iperbole apparirebbe come trasformata della circonferenza in una omologia.
Proiezione di figure poligonali
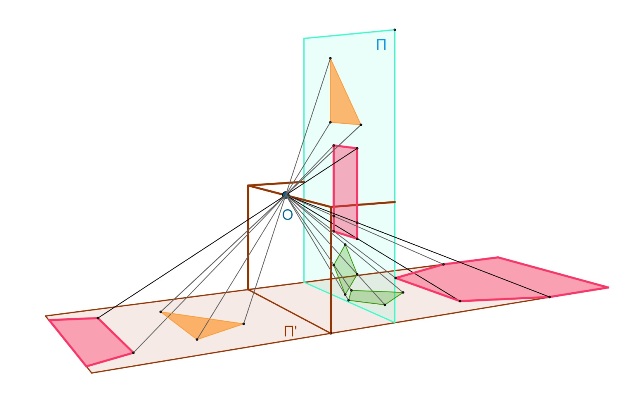
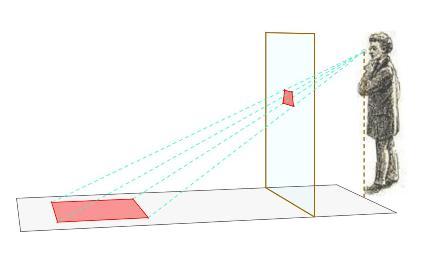
Si osservano due piani incidenti π e π‘ uno dei quali (π ) viene proiettato sull’altro ( π') da un punto O esterno ad entrambi. Alcuni fili tesi collegano coppie di punti corrispondenti al centro di proiezione O. La formazione dell’immagine prospettica e dell’ombra di una figura piana sono casi particolari della corrispondenza più generale illustrata da questo modello fisico.
Il modello mostra inoltre :
- che è possibile muovere il centro di proiezione O assieme al piano π in modo che le coppie di punti corrispondenti restino invariate e allineate con O durante il movimento (Teorema di Stevin).
che i punti di π giacenti da parti opposte rispetto alla retta intersezione tra π e il piano parallelo a π’ passante per O (retta limite di π) vengono proiettati su π' in semipiani opposti aventi come origine comune la retta di intersezione tra π e π' (retta luogo di punti uniti). A rette su π corrispondono rette su π’, ma il parallelismo non è conservato.