Ellissografo ad antiparallelogramma

G

Fig.1

Fig.2

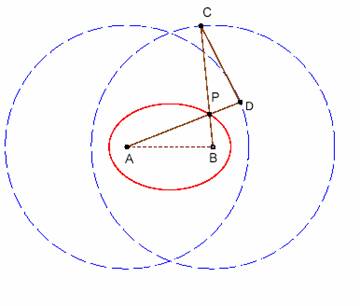
Si dimostra facilmente che nell’antiparallelogramma ABCD (ove AB =CD, AD=CB e AB è fissato al piano) i vertici sono simmetrici rispetto alla bisettrice dell’angolo APC (e del suo opposto al vertice) (fig.1). Ne consegue che PC=PA e che PA+PB=PC+PB=BC= cost., quindi P descrive un’ellisse di fuochi A e B.

Facendo assumere all’ellissografo la posizione in cui l’asta AD si sovrappone al lato (fisso) AB si può verificare che l’asse maggiore dell’ellisse ha lunghezza uguale a quella dell’asta AD; quando CD è parallelo ad AB e quindi P appartiene all’asse del segmento AB è possibile calcolare la lunghezza dell’asse minore.

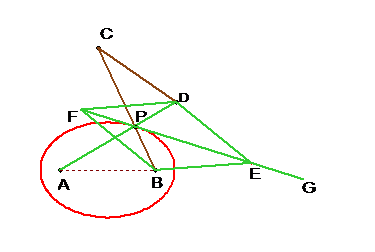
L’antiparallelogramma articolato può essere sostituito con un rombo articolato BEDF (fig.2) avente uno dei vertici (B) imperniato al piano e il vertice opposto incernierato in D all'asta AD. Il vertice E del rombo è scorrevole lungo l'asta mobile FG. Il punto tracciatore P è posto sulla intersezione delle aste AD e FG.

Durante il movimento della macchina il punto P si mantiene equidistante da C e da A (fig.1). Indicata con G la circonferenza descritta da C e convenendo di definire "distanza" di un punto P da una circonferenza G la minima distanza di P da G(valutata quindi sulla retta del raggio passante per il punto) si perviene alla seguente definizione di ellisse :

data una circonferenza G (di centro B e raggio a ) e un punto A interno ad essa, il luogo dei punti equidistanti da A e da G è una ellisse avente i fuochi in B e in A e l'asse maggiore uguale ad a.La circonferenza si chiama cerchio direttore dell'ellisse .

Anche l'iperbole potrà essere definita come luogo dei punti equidistanti da una circonferenza data e da un punto dato esterno ad essa.