Simmetria centrale
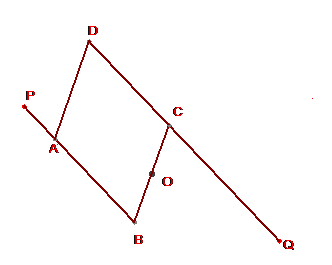
Il sistema è formato da un parallelogramma
articolato ABCD, il cui lato BA è prolungato di una lunghezza AP (qualsiasi) mentre
il lato DC è prolungato di una lunghezza CQ=BP. Il punto medio O del
lato BC è imperniato al piano. I punti corrispondenti P e Q hanno due gradi di
libertà e l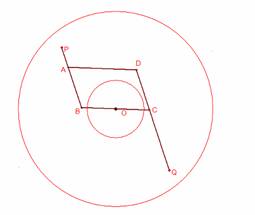a 
corrispondenza
fra P e Q è una trasformazione geometrica.
Le regioni piane messe in
corrispondenza si possono individuare nei seguenti modi:
1) Deformiamo il rombo in modo
tale che i punti P e Q abbiano distanza minima da O: ruotando il sistema
attorno ad O , possiamo osservare che i punti interni alla circonferenza di
centro O e raggio PB-OB sono
inaccessibili a P e Q.
Deformiamo il rombo in modo tale
che i punti P e Q abbiano distanza massima da O: ruotando il sistema attorno ad
O possiamo osservare che i punti esterni alla circonferenza di centro O e
raggio PB+OB sono inaccessibili a P e Q. Le regioni piane messe in
corrispondenza quindi sono sovrapposte e coincidono con la corona circolare di
centro O , raggio interno PB-OB e raggio esterno PB+OB.
Muovendo la macchina è possibile
osservare che i punti P e Q sono, in
ogni posizione, allineati con O e ad ugual distanza da O (i triangoli PBO e QCO
sono congruenti) : la trasformazione generata è una simmetria centrale.
Variando le lunghezze dei lati del parallelogramma
articolato e di AP, non cambia la natura della trasformazione, ma solo la
dimensione delle regioni piane messe in corrispondenza.
Se assumiamo poi PB=OB la corona circolare diviene il cerchio di
centro O e raggio CB: il punto O è accessibile a P e Q, permettendo di
verificare che è punto unito della trasformazione.
