PROIEZIONI DI CONICHE: ELLISSE

.

A partire dai primi decenni del Seicento, dopo gli studi fondamentali di G. Del Monte, B. Pascal e G. Desargues, la trattazione delle coniche viene inserita entro la teoria delle proiezioni.
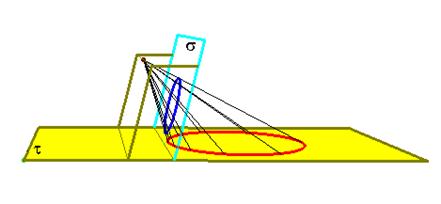
Le coniche infatti si possono considerare come ombre (o prospettive, o anamorfosi) delle circonferenze.

In questo modello fisico i fili tesi possono essere interpretati sia come  raggi visuali convergenti all’occhio di un osservatore, sia come raggi luminosi uscenti da una sorgente puntiforme. Essi stabiliscono una corrispondenza tra i piani incidenti s e t: sono corrispondenti i punti collegati dal medesimo filo. Possiamo anche dire: ogni filo proietta un punto di s in un punto di t; centro di proiezione è il punto di convergenza dei fili.

Il modello mostra che la circonferenza giacente sul piano  s  è proiettata sul piano t da un  centro proprio (non appartenente né a s né a t)  in modo da ottenere una ellisse. Possiamo anche dire: la circonferenza è immagine prospettica dell’ellisse; l’ellisse è ombra della circonferenza.

Il piano della circonferenza e il centro di proiezione possono essere ruotati contemporaneamente per mezzo di un parallelepipedo articolato in modo tale che la corrispondenza tra ellisse e circonferenza rimanga invariata. (Teorema di Stevin). Si noti che s ruota attorno alla propria intersezione con t (retta luogo di punti uniti).