|
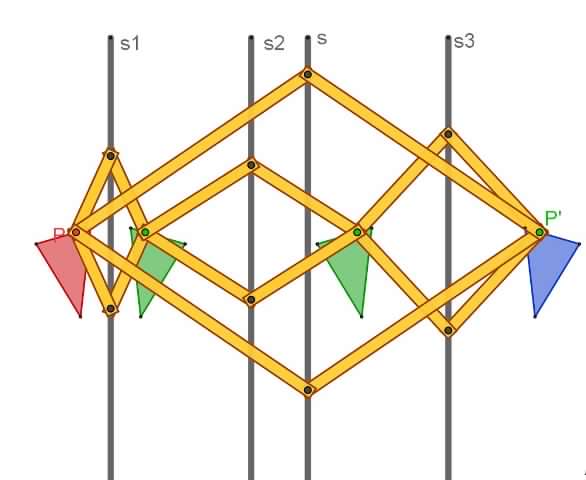 |
La macchina illustra il seguente teorema: "Il prodotto di tre simmetrie assiali ortogonali con assi di simmetria paralleli e aventi distanze assegnate è una simmetria assiale ortogonale con asse parallelo ai tre precedenti e avente dal primo distanza uguale a quella fra il secondo e il terzo". Tre macchine per la simmetria assiale ortogonale di assi paralleli s1,s2,s3 e aventi distanze assegnate d(s1,s2)= h e d(s2,s3)= k sono collegate in modo da realizzare il prodotto delle tre simmetrie . Una quarta macchina per la simmetria, con asse s parallelo ai precedenti e fissata al piano in modo che d(s1,s)=d(s2,s3)=k è applicata ai punti P e P’ corrispondenti nel prodotto delle tre simmetrie . Muovendo P si osserva che tutto il sistema articolato si pone in movimento senza bloccarsi verificando localmente in tal modo un caso particolare del teorema.