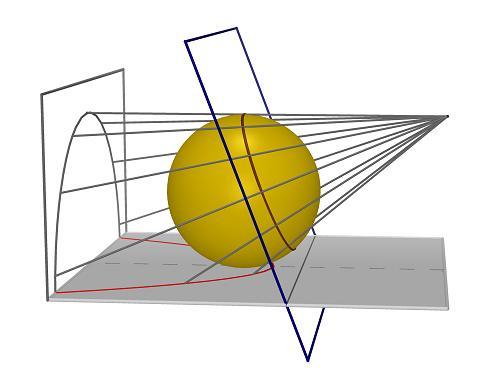
"Esistono due sfere iscritte in una superficie conica rotonda e tangenti ad un piano π(che la interseca e non passa per il vertice) se l’angolo θ della superficie conica (angolo acuto costante fra l’asse della superficie e una delle sue generatrici) non è uguale all’angolo φ formato dall’asse della superficie col piano π : in questo caso il piano π individua sulla superficie conica una ellisse oppure una iperbole. Se invece θ = φ(caso della parabola) esiste una sola sfera tangente a π. I punti di contatto delle sfere inscritte nella superficie conica e tangenti al piano πdella sezione si dicono fuochi della conica. Si chiama direttrice corrispondente ad un fuoco la retta comune a πe al piano che passa per il circolo di contatto della superficie conica con la sfera iscritta corrispondente al fuoco stesso. Quindi mentre ogni ellisse ed ogni iperbole ha due fuochi e due direttrici, ogni parabola ha un solo fuoco e una unica direttrice."
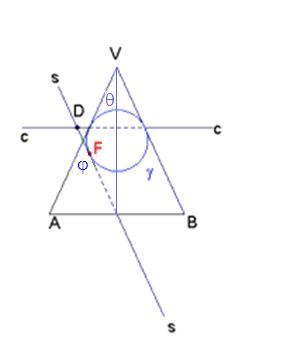
In the picture, VAB is the axial triangle obtained by cutting the cone with a plane containing the axis, circumference γ is the intersection between this same plane and the Dandelin\'s sphere, straight line cc is the intersection between the plane containing the triangle and the plane containing the cone-sphere contact circle (the dashed part is the diameter of the circle), straigt line ss is the intersection between the plane containing the triangle and the plane containing the cone section (the segment inside the triangle is the parabola\'s axis), F is the parabola\'s focus, running through D, perpendicularly to the plane containing the triangle, is the parabola\'s directrix.
Hyperbola
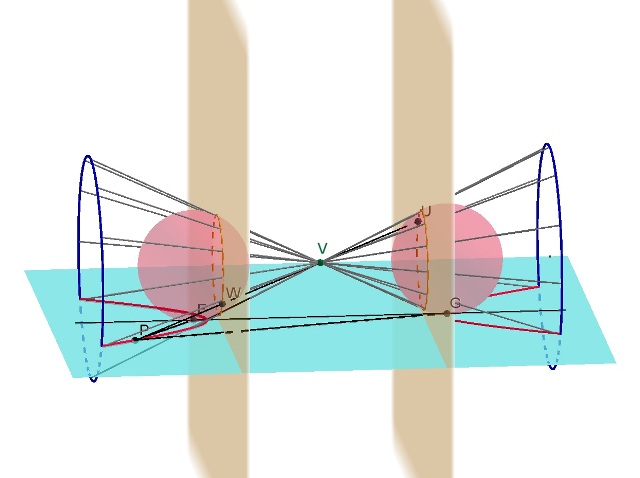
PG=PU (the straight lines go through P and are tangent to the sphere)
PF=PW PG-PF=PU-PW=WU (costant)
Ellipse
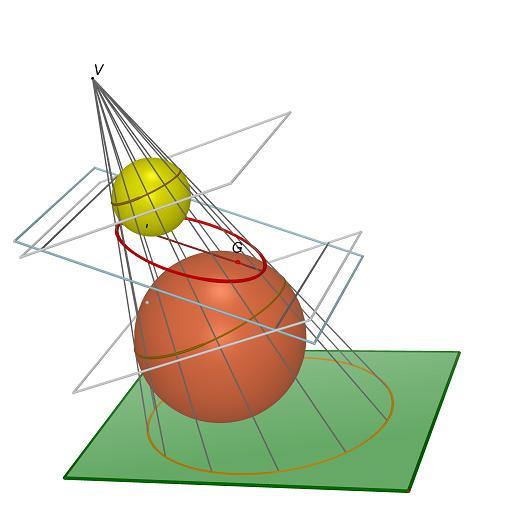
The conic curve along which a round cone is sectioned by a plane has its two focuses in the points where the plane is tangent to the spheres inscribed in the cone. The straight lines obtained intersecting the secant plane with the cone-sphere contact circle are the directirxes of the conic curve (Dandelin - Quetelet, 1822). In the case of the ellipse, two are the spheres with this property: respect to the plane to which the conic belong, one is on the side of the vertex and the other is on the opposite side. Based on the notorious properties of the tangents to a sphere running through a point, the definition of focus of a round cone section that arises from the Dandelin\'s theorem brings to the main properties of the focus points of a conic curve. While most of the studies on conics, as curves concieved in the 3D space, are based on projective goemetry, Dandelin and Quetelet go back to classical geometry finding new properties missed by previous researchers. A meaningfull difference has anyway to be pointed out: while the original wording describes the theorem as \"static\" (and the same is for the model that illustrates it), Quetelet and Dandelin research is based on geometry of movement and more precisely on the study of \"focal curves\", therefore those curves (strophoids) described by the ellips focuses when the secant plane rotates around one of the two straight lines tangent to the cone.
In the picture below, VAB is the axial triangle obtained by cutting the cone with a plane to which the axes of the cone itself belongs.
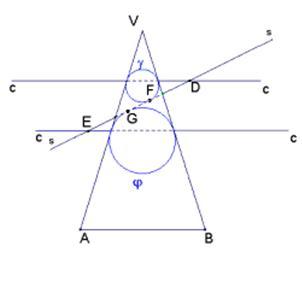
Circumferences Υ and φ are the intersections between those planes and the Dandelin spheres. Straight lines cc are the intersections between the plane containing the triangle and the plane containing the cone-sphere contact circle (two in this case). The dashed segments are the diameters of the contact circles. Straight line ss is the intersection between the plane containing the triangle and the plane containing the conic section. The dashed segment is the majior axes of the ellipse. F and G are the focal points of the ellipse. The directixes of the ellipse, relative to the focal points, go through D and E, perpendicularly respet to the plane containing the triangle.